回帰を理解する
まず、回帰分析と機械学習や統計の世界でよく聞くかもしれませんが、説明してと言われた場合はどう言いますか?
今回は回帰分析を理解できるようになりましょう!
回帰分析とは
ある変数と他の1つの変数または複数の変数との関係をみる分析手法です。
例を使ってもう少し理解していきましょう!

「収入を上げたいなー。どんな人が収入高いのか知りたいな。」

「収入と関係しそうな要素が何か考えてみましょう!」

「うーん。日本だと年齢とかかな。」

「そうですね!これで回帰分析する情報が集まりました。」
まとめ:収入は年齢とどのような関係かみるのが、回帰分析と言えます!
線形回帰
ある変数と1つの変数の関係をみるものです。
これは先ほどの例でいうと、収入に年齢という1つの変数が関係を確認するというものです。
このオレンジが回帰分析のイメージでしょうか (^ ^)
収入と年齢の関係
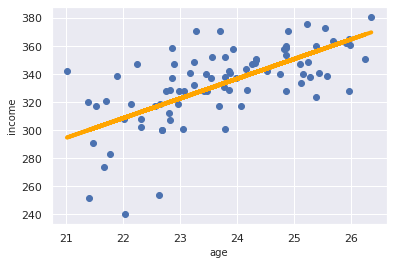
補足ですが、上記のグラフはpythonのmatplotlib、seabornのライブラリで作成しています。
式で表すと y=β0+β1 x(β0は切片はβ1は傾き)の一次関数となります。
重回帰
ある変数と複数の変数の関係をみるものです。
収入の例でいうと年齢以外の要素、勉強時間、会社の規模(大企業、中小企業)も収入に影響があると考えられます。
そのような複数の要素で収入を説明するイメージです。
重回帰分析は先ほどの単回帰分析と異なり、3次元より大きくなる場合は、グラフで可視化できなくなります。
式で表すと y=β0+β1 X1+β2 X2+β3 X3+・・+βk Xk (β0は切片、β1~βkは関係する要素)の多次元関数となります。
<補足>
重回帰分析が可視化できないので、どのように結果の妥当性をみるのか?という疑問が出るかもしれません。
それは決定係数の値で確認します! 以下のようなイメージです。
R2(決定係数)= 説明できるばらつき / 全体のばらつき
決定係数は上記の式のイメージから分かる通り、0 ~ 1の範囲の値で大きい程、良い精度だと言えます(^ ^)
少しはイメージできたでしょうか。
もう少し理解を深くしたい方は以下の本が評価高くておすすめです。
 |
新品価格 |
![]()
まとめ
回帰分析はよく聞くかもしれませんが、どのような時に使われると整理できるようになれば使いこなせていくかと思います。
機械学習でもよく、予測分析等で用いるので、覚えておくといいと思います!
それでは今日はここまで。
プログラミングを始めようと思った際は独学で勉強すると挫折する可能性が高いため、スクールも考えてもいいと思います!