機械学習の際に必要な概念
まず最初に機械学習はすべてのデータで活用できるかと言えば、そうではありません。
人間でも判断できないもの。
例えば、今日買った宝くじに当たるか当たらないか。10年後に自分は生きているか死んでいるか。
家族や知り合いが今、ほしいものは何か。
上記のような「これだ」という回答ができないようなことや少ない情報量のデータしかないような場合は機械学習を活用することは難しいです。
逆にデータ数が多く、何かしらの「パターン」を見つけられるようなデータ。
例えば、① ある飲食店の売上商品データ、② youtubeでの1年間の視聴履歴、③ 電気料金の5年間の推移と気温データ等。
| 機械学習で使用できるデータ例 | 分かること（特徴） |
|---|---|
| ある飲食店の売上商品データ | 商品別の売上ランキング |
| youtubeでの1年間の視聴履歴 | 興味あるジャンル |
| 電気料金の5年間の推移と気温データ | 気温ごとの電気料金の関係性 |
上記のように何かデータから特徴を見つけられるそうなデータは機械学習を効果的に活用することができます。
機械学習ということを理解していない方はこちらを参照ください。
特徴量
上記のように効果的に機械学習を用いるデータがあった場合に知りたい対象を数値化したものを「特徴量」といいます。
この特徴量を用いて機械学習では予測や分類をしています。
この特徴量の数を次元といいます。
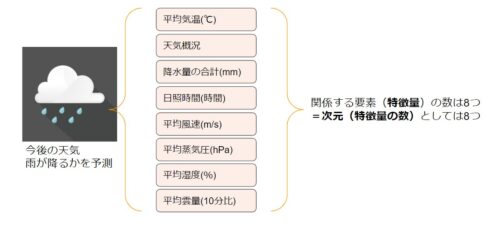
分かりにくいので、例えでいうと仮に予測したいものが今後の天気（雨が降るか）とするとそれに関係する要素である気象データ「平均気温(℃)、天気概況(昼：06時～18時)、降水量の合計(mm)、日照時間(時間)、平均風速(m/s)、平均蒸気圧(hPa)、平均湿度(％)、平均雲量(10分比)」のように複数あることが多いです。
今回のように天気に関する（雨が降るか）に関係するデータの数が8つの場合は次元数は8つとなります。
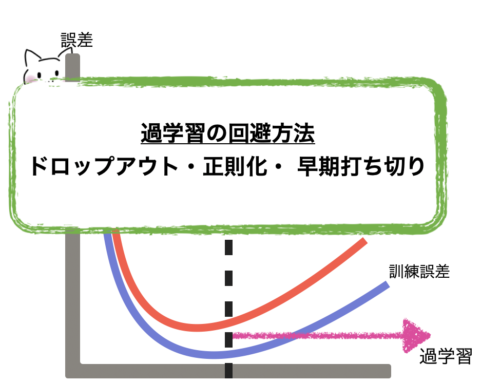
次元の数が多くなればなるほど学習するデータの特徴を忠実に再現（過学習）し、誤差を許容せず、予測精度を下げる可能性があります。
過学習に関しては以下の記事を参考にしてください。
過学習とは機械学習で学習させすぎて、訓練データでは正解率が高いが、訓練データ以外だと正解率が下がってしまう事です。つまり、訓練データだけに最適化されてしまい、汎用性がなくなる事です。特にニ[…]
また次元数が多いほど予測の計算処理に時間がかかることもあり、その対策として主成分分析（PCA）というものが用いられます。
主成分分析（PCA）
principal component analysisの略語で次元削減とも言われます。
一言でいうと機械学習の「関係するデータの数を絞る」ということです。
これはイメージでいうと、今後の天気（雨が降るか）とするとそれに最も関係する深い要素である気象データで機械学習を実施する。
つまり特徴量の数を8つ⇒2つ（8つより少なく）にする感じです。
それにより柔軟な予測ができたり、処理速度を上げることにもなります。
※もし関連しない、関連性が低い項目の場合は予測精度は下がります。
主成分分析（PCA）では最もデータに対して関連性が高い直線を探して、誤差の二乗が一番小さいところで最適に引くことが第1主成分と言わます。
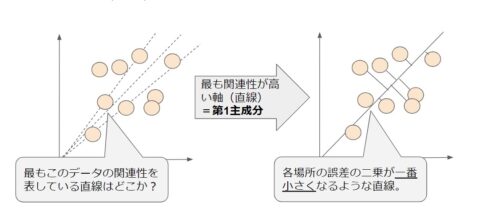ただ、それだけではデータの誤差（機械学習で考慮されない要素）を含んでしまうため、第2主成分となるような直線を引きます。
主成分自体は第3,４主成分等もありますが、あくまで関連性が高い順に並べて機械学習することを目的にしています。
誤差が少なければ機械学習の予測精度もよいです。
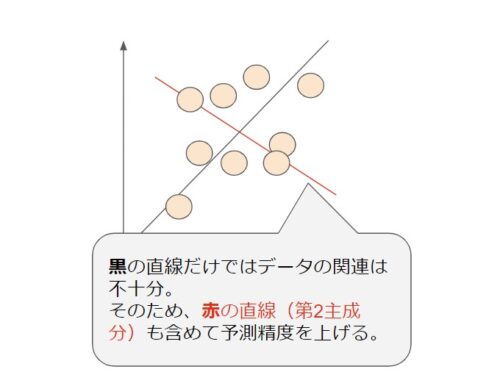
今回の例え話の今後の天気（雨が降るか）とするとそれに最も関係する深い要素である気象データを2つにする場合であれば第2主成分のみまでとなります。
これが関係するデータの数を絞るというイメージとなります。
まとめ
今回出てきた単語をまとめていきます。
「特徴量」＝知りたい対象を数値化したもの（例：天気予測したい場合は、気温、湿度等が特徴量）
「次元」＝特徴量の数
「主成分分析（PCA）」＝関係するデータの数を絞る（最も関連する特徴量から第1主成分、第2主成分..という順番になる）
少しでもイメージができれば幸いです。
